Utlizing different gap penalties for different human genomic regions

In next several blogs, I will write things about my Ph.D. work. The first topic today is highly related to our work Vulcan, which utlizes 2 different kinds of gap penalties for better long-read alignments.
Different regions in human genome may have different mutation rates, here are some examples:

• Housekeeping genes usually have low mutaion rates, which means they are evolving slower than the others.
• Genes involved in immune responses, tend have higher mutation rates.
• In the population scale, there are also genes divergent among people such as LPA genes and Cyp2d6 genes.

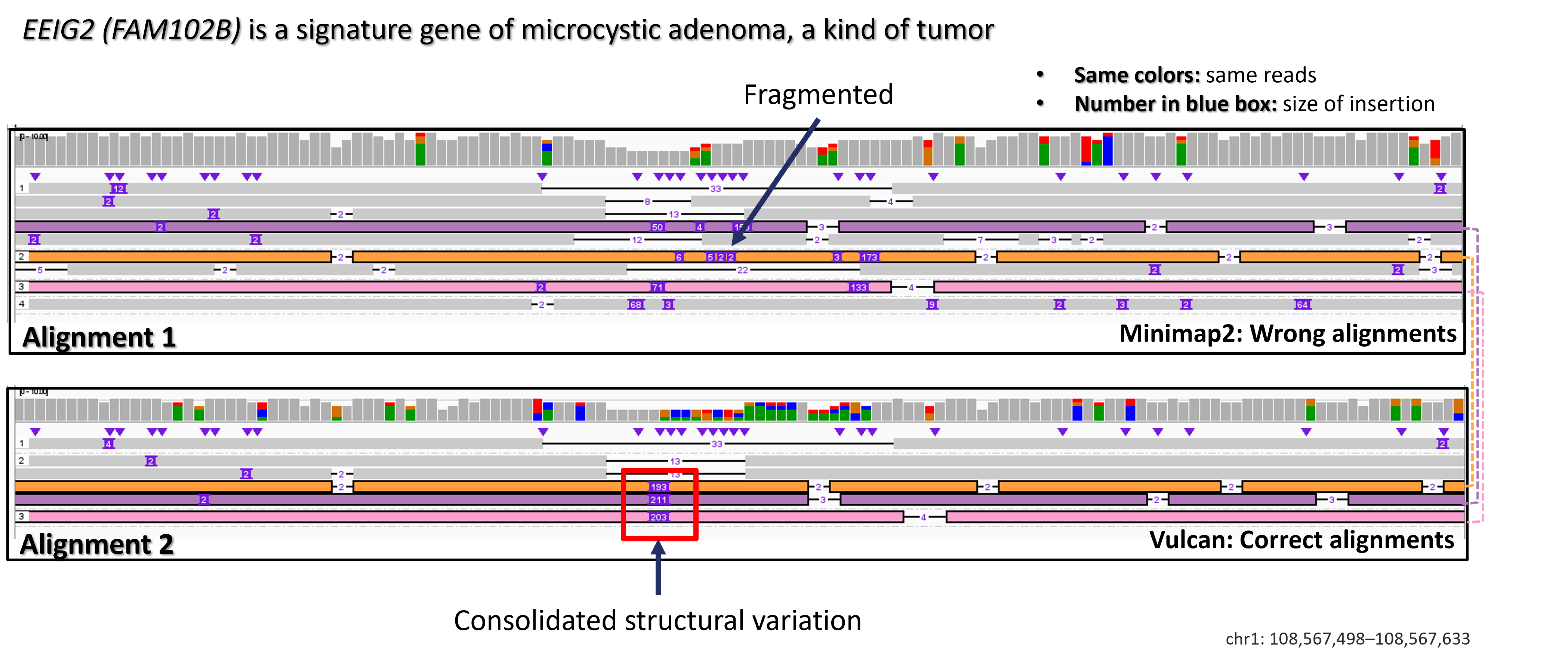
We all know that long-read sequencers suffers from sequening errors, and those sequencing errors may have different effects on alignment accuracy when we are trying to align reads to these differnet regions. In this case, using the same gap penalty maybe not sufficient for all those different regions. For example, in this case, 2 different gap penalties made different choices in EEIG2 gene. Gap penalties mainly alter the pairwise alignment behaviors in the extension stage during long-read alignment process. The state-of-the-art long-read aligners use either affine gap penalty (minimap2) or convex gap penalty (NGMLR).
What is the difference between these two penalties?

• Affine gap penalty calculates alignment scores as \(G(i) = g_o + g_E * i\)
• Convex gap penalty calculates alignment scores as \(G(i)=\left\{\begin{matrix}g_o,i=0 \\ G(i-1)+min\left\{\begin{matrix}g_M \\ g_E+g_D*(i-1) \end{matrix},i>0\right. \end{matrix}\right.\)

In here, \(g_o\) : gap opening penalty; \(g_E\) : gap extension penalty; \(g_M\) : gap matching score; \(i\) : current length of the gap; \(g_D\) : gap decay parameter between 0 and 1; \(m\) and \(n\) are the length of two sequences. We can clearly see that the time complexity of affine gap penalty is \(O(mn)\) while the one for convex gap penalty is \(O(mnlog(m+n))\) since it need to remember the scores from previous gaps.
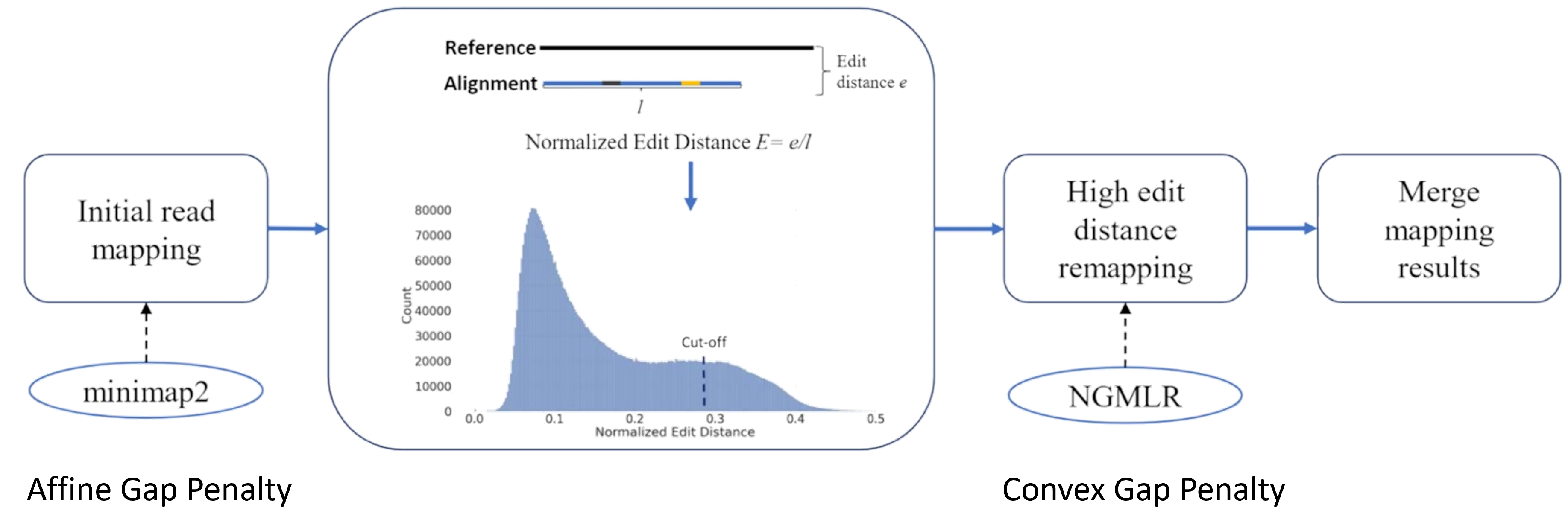
Due to the gap decay parameter, convex gap penalty funcitons always favor larger gaps than smaller ones. In NGMLR paper they claims this kind gap penalty helps long-read aligner to become more robost against sequencing errors. However, is this entirely true? We think when we are aligning reads to the regions where the sequencing errors are dominant “variants” against the reference, affine gap penalty can actually work better, and in these regions the edit distances between reads and the reference are usually low since there are fewer variations. Based on that, we can filter the read alignment that have high edit distance from minimap2 and put those into NGMLR for re-alignment.
Based on this motivation, we developed Vulcan: